Jak Obliczyć Natężenie Pola Elektrycznego w Centrum Kołowej Obręczy?
Czasem wydaje się, że fizyka to tylko teoria i równania, które trudno sobie wyobrazić. Ale co, jeśli powiedziałbym Ci, że wystarczy „rozłożyć” obręcz na maleńkie fragmenty, by wszystko stało się prostsze? W tym artykule wyjaśnię, jak obliczyć natężenie pola elektrycznego w punkcie o współrzędnych (0,0,h), i to w sposób przyjazny i wesoły. Gotowy na przygodę z elektrostatyką?
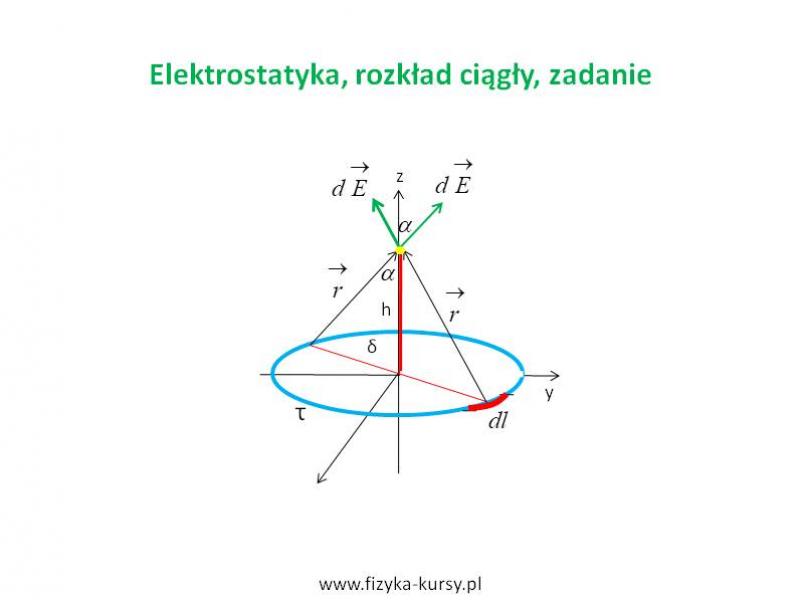
Treść zadnia: Podczas doświadczenia naładowałeś jednorodnie kołową obręcz o promieniu „δ” ładunkiem dodatnim o gęstości liniowej τ C/m. Układ wygląda tak jak na rysunku poniżej. Oblicz jakie jest natężenie pola elektrycznego w miejscu o współrzędnych (0,0,h).
Co to znaczy „rozłożyć na drobne kawałki”? – Sekret ciągłego rozkładu!
Co to jest rozkład ciągły?
Wyobraź sobie obręcz naładowaną pozytywnym ładunkiem o gęstości liniowej τ (wyrażonej w C/m). Zamiast jednego dużego ładunku, mamy tutaj setki, tysiące, a nawet miliony drobniutkich ładunków, które tworzą rozkład ciągły. Każdy z tych malutkich ładunków wpływa na natężenie pola elektrycznego. W takich zadaniach nie analizujemy jednego punktu, ale całą masę ładunków. Do tej pory analizowaliśmy tylko jeden ładunek lub maksymalnie kilka. W tych zadaniach będziemy analizować układy, na których jest zgromadzona bardzo duża ilość ładunku. Z tym jest związana podstawowa różnica, którą widać na pierwszy rzut oka, już na etapie czytania treści zadania. Do tej pory w treści zadania miałeś podawaną wartość ładunku prawda? Od teraz w tego typu zadaniach będzie podawana gęstość ładunku, czyli informacja mówiąca o ilości ładunku na m, m2 lub m3.
Dlaczego musimy scałkować cały układ?
Aby obliczyć natężenie pola elektrycznego, musimy najpierw… rozłożyć obręcz na maleńkie kawałeczki! Każdy kawałek odpowiada za mikroskopijną część pola elektrycznego, które później zsumujemy (czyli scałkujemy) w jeden, większy wektor. Ten nieskończenie mały wycinek tego pierścienia ma na swojej powierzchni zgromadzoną nieskończenie małą wartość ładunku, która z kolei powoduje powstanie nieskończenie małego natężenia pola elektrycznego w żółtym punkcie. Zielona strzałka pokazuje kierunek i zwrot tego natężenia.
Symetria – klucz do uproszczenia obliczeń!
Czy symetria naprawdę ma aż tak duże znaczenie?
Tak, symetria to nasz najlepszy przyjaciel! Jeśli spojrzysz na rysunek, zauważysz, że każdy fragment pierścienia ma swój „odpowiednik” po drugiej stronie, co pozwala nam na uproszczenie obliczeń. Wszelkiego rodzaju koła, pierścienie czy kule są symetryczne. Co to znaczy? To oznacza to, że dokładnie po drugiej stronie pierścienia jest również nieskończenie mały element, który generuje dokładnie taką samą wartość natężenia pola elektrycznego, ale o przeciwnym zwrocie na osi X i Y. To znaczy, że jak rozłożymy zielone wektory na składowe, to składowe na osi X i Y skrócą się. Zostaną tylko składowe na osi Z.
Właśnie dlatego od razu możemy napisać, że składowe Ex i Ey równają się zero.
Jak policzyć natężenie pola na osi Z?
Krok 1: Oblicz długość wektora dE
Najpierw musimy obliczyć długość wektora dE, który będzie nam potrzebny do dalszych wyliczeń. Skorzystamy tutaj z podanej gęstości ładunku, a następnie przekształcimy wyrażenie, by obliczyć wartość dE.
Idźmy tym samym tokiem myślenia co w poprzednim zadaniu link Zadania elektrostatyka Obliczmy najpierw długość wektora , a dopiero później zastanowimy się nad kierunkiem i zwrotem. Długość wektora obliczymy z poniższego wzoru. Dodatkowo od razu wykorzystałem informację odnośnie gęstości ładunku. Jak wymnożę gęstość ładunku razy nieskończenie mały wycinek to otrzymam nieskończenie małą wartość ładunku. Trzeba teraz wstawić te przekształcenia do wzoru na natężenie.
Po podstawieniu wygląda to tak:
Co my tutaj otrzymaliśmy? Otrzymaliśmy wzór, z którego moglibyśmy obliczyć długość wektora dE. Z tym, że my mamy obliczyć wektor natężenia pola elektrycznego prawda?
Krok 2: Składowa na osi Z
Pamiętasz, że składowe na osiach X i Y się skróciły? To oznacza, że pozostała nam tylko składowa na osi Z. Patrząc na rysunek widać ewidentnie, że składową na osi Z można obliczyć korzystając z kosinusa.
Z poniższego wyrażenia moglibyśmy obliczyć składową na osi Z.
Z treści zadania nie znamy „r” ani kąta. Musimy to zastąpić przez inne wyrażenia. Poniżej przekształcenia.
Ok. Można już podstawić wyrażenia z czerwonej ramki do wcześniejszego wzoru. Po wykonaniu podstawień otrzymujemy wzór na dEz.
Wszystko byłoby już fajnie, ale z tego wzoru to my, co najwyżej, obliczymy składową na osi z nieskończenie małego wektora dE. A my przecież mamy obliczyć natężenie pola elektrycznego pochodzące od całego pierścienia , a nie tylko od jego nieskończenie małego wycinka. W takiej sytuacji oczywiście musimy zsumować wszystkie nieskończenie małe natężenia pochodzące od wszystkich nieskończenie małych elementów. Do sumowania nieskończenie mały elementów służy oczywiście całka.
Poniżej rozwiązanie
Chcesz wiedzieć więcej? Obejrzyj mój kurs i zobacz film!
Jeśli zainteresował Cię temat elektrostatyki i chciałbyś poznać więcej takich zadań, zapraszam Cię do mojego kursu online z teorii pola elektromagnetycznego oraz elektrostatyki. Znajdziesz tam mnóstwo przykładów i praktycznych wskazówek, które rozwieją wszelkie wątpliwości. Oto linki do kursów oraz film na YouTube:
- Kurs: Teoria Pola Elektromagnetycznego – część 1
- Kurs: Elektrostatyka
- YouTube: Link do filmu