Prawo Coulomba – Fizyka z Uśmiechem
Co to jest Prawo Coulomba i dlaczego jest takie fascynujące?
Zanim zanurzymy się w fascynujący świat Prawa Coulomba, musimy wyjaśnić kilka podstawowych kwestii. Wyobraź sobie, że podobieństwa się odpychają – to znaczy, dwa dodatnie ładunki oraz dwa ujemne ładunki wzajemnie się odpychają. Z kolei różnoimienne ładunki przyciągają się jak magnesy! Popatrz na tę uroczą grafikę poniżej – czujesz już tę elektryczną chemię?
Trochę historii – Charles Coulomb, nie mylić z Kolumbem!
Zjawiska przyciągania i odpychania ładunków elektrycznych obserwowano od wieków, na przykład przy elektryzowaniu włosów podczas zdejmowania swetra. Ale naukowcom takie zjawiska to za mało! Oni muszą wszystko opisać za pomocą wzorów. Charles Coulomb (nie mylić z Krzysztofem Kolumbem, tym od Ameryki) przeprowadził kilka eksperymentów i odkrył, że siła przyciągania lub odpychania dwóch ładunków elektrycznych zmniejsza się odwrotnie proporcjonalnie do kwadratu odległości między nimi oraz jest wprost proporcjonalna do wartości tych ładunków. Brzmi skomplikowanie? Nie martw się, zaraz to uprościmy!
Prawo Coulomba – oto magiczny wzór!
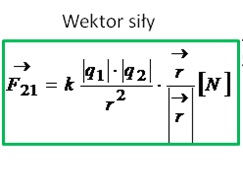
Oto wzór, który stanowi esencję Prawa Coulomba. Poniższy wzór odnosi się do wartości siły. Wartość siły to jest dokładnie to samo co długość wektora, a długość wektora oznaczamy w takich dwóch kreskach pionowych tak jak niżej.
Powyższy wzór to jest kwintesencja prawa Coulomba. Z tego wzoru ewidentnie widać, że im większa wartość ładunków tym większa wartość siły oddziaływania między nimi (tak wygląda proporcjonalność) wartość siły oddziaływania dwóch ładunków maleje wraz ze wzrostem odległości między nimi i to maleje z kwadratem odległości (gdyby „r” nie było podniesione do kwadratu to można by powiedzieć, że siła maleje odwrotnie proporcjonalnie do odległości).
Dlaczego warto to wiedzieć? Bo im większe ładunki, tym większa siła oddziaływania między nimi. A im większa odległość między ładunkami, tym mniejsza siła – i to maleje z kwadratem odległości! To tak, jakby siła była na diecie – im dalej, tym bardziej chudnie.
Czujesz déjà vu? Prawo Coulomba a prawo grawitacji
Tak, tak, wzór Prawa Coulomba wygląda podejrzanie znajomo. Jeśli myślisz, że gdzieś już to widziałeś, to masz rację!
Prawo Coulomba przypomina prawo powszechnego ciążenia. Spójrz na podobieństwa:
- W obu wzorach mamy stałą przed ułamkiem: „k” w Prawie Coulomba i „G” w prawie ciążenia.
- W mianowniku każdego ułamka mamy „r” (odległość) podniesione do kwadratu.
Warto zwracać uwagę na takie podobieństwa, bo dzięki temu łatwiej się tego nauczyć!
Czas na zabawę – praktyczne zastosowanie Prawa Coulomba
Teoria teorią, ale czas na praktykę! Zróbmy razem kilka obliczeń, aby zobaczyć, jak Prawo Coulomba działa w prawdziwym świecie. Gotowy na trochę matematycznej magii? Liczymy razem!
Zadanie z elektrostatyki cz.1
Oblicz wartość siły F12 Wzoruj się a rysunku poniżej.
Jeśli mamy obliczyć wartość siły to na pewno wato napisać sobie wzór na wartość siły, który przestawiłem powyżej.
Stałą „k” znamy (napisałem ją powyżej), wartości ładunków również, odległość również. A więc mamy wszystko co potrzebujemy, żeby obliczyć wartość siły oddziaływania dwóch ładunków ze sobą. Podstawmy dane i dokończmy obliczenia.
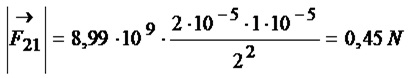
Wartość siły jest równa 0,45N.
Zadanie z elektrostatyki cz.2
Ok. Wcześniejsze zadanie udało nam się obliczyć. Teraz proponuję żebyśmy korzystając z dokładnie tych samych danych obliczyli, ile jest równy wektor siły, a nie tak jak do tej pory wartości siły, czyli jej długość.
Żeby otrzymać współrzędne wektora siły to można to zrobić na dwa sposoby. W tym artykule pokażę Ci tylko jedną z nich (powiedziałbym, że ta metoda jest taka bardziej studencka). Zacznijmy od tego, że każdy wektor posiada trzy cechy tj. długość wektora, zwrot i kierunek. Długość wektora to już wiemy, jak obliczyć. Ale żeby otrzymać współrzędne to musimy jeszcze tej długości przypisać kierunek i zwrot. Można to zrobić mnożąc długość wektora razy wektor jednostkowy, który będzie miał dokładnie taki zwrot jak siła. Pokazuje to wzór poniżej
W tym celu nasz układ z ładunkami musimy wpisać w układ współrzędnych. Najlepiej jeden z ładunków umieścić w początku układu współrzędny wiec jego współrzędne są równe [0,0] natomiast ładunek q2 jest oddalony o 2 metry od pierwszego wiec jego współrzędne muszą być równe [2,0].
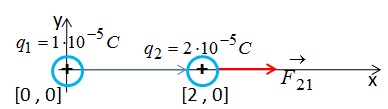
Odległość między ładunkami można przedstawić za pomocą wektora (na rysunku powyżej to jest niebieska strzałka). Jak współrzędne tej niebieskiej strzałki podzielimy przez jej długość to otrzymamy wektor jednostkowy, czyli wektor, którego długość będzie równa 1. Mnożenie razy 1 generalnie nic nie zmienia, ale wektor jednostkowy oprócz tego, że jego długość jest równa 1 to niesie on również informacje o kierunku i zwrocie, a jego kierunek i zwrot tak jak widzisz jest dokładnie taki sam jak kierunek i zwrot czerwonej siły.
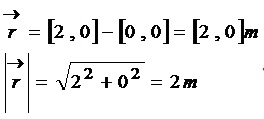
Podstawmy dane do wzoru
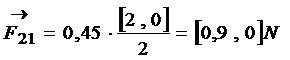
No i mamy wszystko:) Zadanie rozwiązane.
Szukasz więcej zadań tego typu? Zapraszam do mojego kursu z elektrostatyki lub do kursu z teorii pola elektromagnetycznego




