Moc czynna, moc bierna, moc pozorna i współczynnik mocy – Zabawne wprowadzenie

Moc elektryczna – magia rezystorów, cewek i kondensatorów!

Zanim zagłębimy się w tajemniczy świat mocy czynnej, biernej i pozornej, musimy zrozumieć, kim są nasi główni bohaterowie: rezystor, cewka i kondensator. To właśnie oni sprawiają, że prąd płynie, a światło świeci, a my wciąż mamy o czym pisać!

Rezystor – grzejnik w przebraniu

Rezystor to taki mały, sprytny kawałek metalu, który uwielbia zamieniać energię elektryczną w ciepło. Gdyby miał swój własny serial, pewnie nazywałby się "Jak zostałem grzejnikiem".

Cewka – magnetyczny wirtuoz

Cewka to inny dziwak – uwielbia gromadzić pole magnetyczne. Pomyśl o niej jak o magiku, który potrafi zwinąć prąd w kłębek i schować go w swoim kapeluszu.

Kondensator – elektryczny chomik

Kondensator to mistrz gromadzenia energii elektrycznej. Gdyby kondensatory miały swoje reality show, nazywałoby się "Chomikowanie z prądem".

Jak te elementy wpływają na opór?

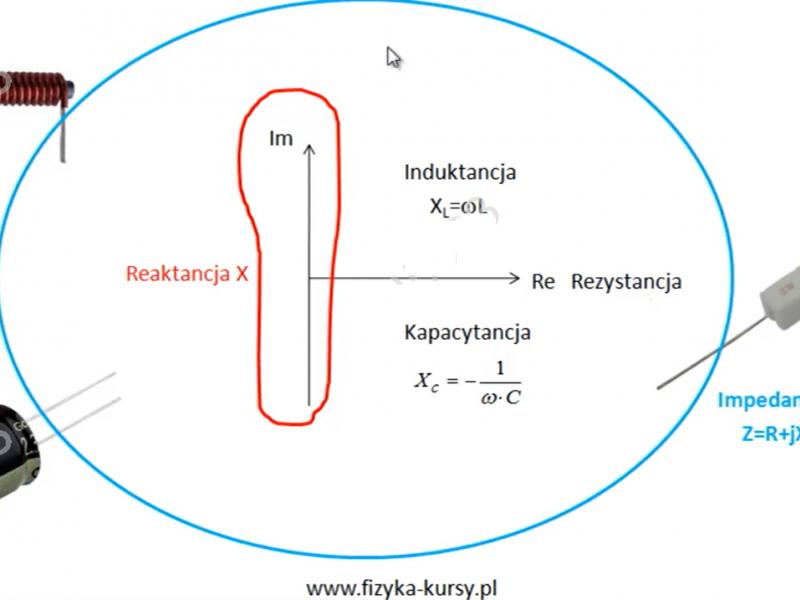
Każdy z naszych bohaterów generuje opór. Ten opór można przedstawić w układzie współrzędnych (oś X i oś Y). Poniżej przestawiłem grafikę to pokazującą. Przyjęło się, że opór od rezystora przedstawia się na osi X podając jakieś konkretne wartości np. 5 Ω, 150 Ω itd. Skoro oś X jest zarezerwowana do rezystorów to oczywistym jest, że oś Y (oś liczb urojonych) musi być zarezerwowana do cewki i kondensatora. „Oporność” elementów urojonych, czyli cewki i kondensatora nazywa się reaktancją. W przypadku dodatniej części reaktancji nazywa się ją induktancją X_L=w*L, natomiast w przypadku ujemnej osi urojonej mamy do czynienia z kapacytancją Xc=-1/w*C.

Impedancja – kiedy świat rzeczywisty spotyka się z urojeniem

Jeśli natomiast w naszym układzie mamy elementy rzeczywiste, czyli rezystory i elementy urojone, czyli cewki albo kondensatory to „oporność” takiego układu nazywa się impedancją ( patrz na grafikę poniżej). Gdy łączymy rezystory z cewkami i kondensatorami, powstaje coś, co nazywamy impedancją – to jak mieszanka rzeczywistości z odrobiną fantazji. Możemy to zobaczyć na wykresie, gdzie opór (rezystancja) spotyka się z reaktancją, tworząc harmonijną symfonię prądu.

Oczywistym jest że każdy z tych elementów może generować moc. W przypadku rezystora to tutaj sprawa jest prosta do wyobrażenia bo rezystor generuje ciepło wiec w jego przypadku mamy do czynienia z mocą cieplną. Pozostałe elementy czyli kondensator i cewka one również generują moc. Można to przedstawić na wykresie tak samo jak „oporności”. Moc elementów rzeczywisty czy czyli rezystorów będziemy przestawiać na osi X, natomiast kondensatora i cewki na osi urojonej (oś Y).

Moc czynna – jak gorąco może być?

Moc czynna to ta część mocy, która zamienia się w ciepło. Wzór na nią jest prosty jak przepis na herbatę:

P=U*I*cosφ [W]

Do powyższego wzoru wprowadza się napięcie i natężenie skuteczne. Kąt φ to kąt przesunięcia fazowego między napięciem i natężeniem.

Moc czynną można też obliczyć z innego wzoru a mianowicie można wymnożyć rezystancję razy natężenie skuteczne podniesione do kwadratu.

P=R*I²

Moc bierna – zakręcony kuzyn mocy czynnej

Moc bierna to ta część mocy, która bawi się w kotka i myszkę z cewkami i kondensatorami. Wzór wygląda znajomo, ale z małym twistem:

Q=U*I*cosφ [Var]

Jak widzisz wygląda on dokładnie tak samo jak na moc czynną z tą różnicą, że w mocy czynnej mieliśmy kosinusa natomiast w mocy biernej mamy sinusa.

Tak samo jak w mocy czynnej moc bierną również można obliczyć w dwóch wersjach. Moc czynna odnosi się do rezystorów i w tej drugiej wersji można było ją obliczyć mnożąc rezystancję z z natężeniem skutecznym. W mocy biernej można zrobić to dokładnie tak samo z tą różnicą że w miejscu rezystancji musimy wstawić reaktancję cewki lub kondensatora (w zależności z czym będziemy mieli do czynienia). Wzór wygląda jak poniżej:

Q=X*I²

Moc pozorna – wszystkie moce w jednym miejscu

Jeśli chodzi o moce to nie wszystko. Mamy oczywiście moc czynną i bierną ale oprócz tego jest jeszcze coś takiego jak moc pozorna. Moc pozorna pojawia się w układach w których mamy elementy rzeczywiste czyli rezystory i elementy urojone czyli cewki i kondensatory. Taki układ złożony z wyżej wymienionych elementów generuje moc która jest sumą mocy czynnej i mocy biernej i ma to swoją oddzielną nazwę nazywa się to mocą pozorną. Jednostką mocy pozornej jest wolto amper [VA]. Już sama jednostka nam podpowiada w jaki sposób można obliczyć moc pozorną. Wystarczy wymnożyć ze sobą napięcie skuteczne które podajemy przecież w woltach z natężeniem skutecznym prądu, które podajemy w amperach.

S=U*I

Tak samo jak dwa wcześniejsze wzory mogliśmy obliczyć na 2 sposoby tak samo i tym razem. Jedyna różnica jest taka że w miejscu w którym mamy „oporność” tym razem w przypadku mocy pozornej musimy wstawić impedancję

S=Z*I²

Moc pozorna zespolona – gdy prąd przemienny spotyka liczby zespolone

W na zajęciach najczęściej będziesz operował prądem przemiennym. Obliczenia na prądzie przemiennym najlepiej prowadzić na liczbach zespolonych. W świecie prądu przemiennego, moc pozorna zespolona to prawdziwy hit. Aby ją obliczyć, wystarczy wymnożyć napięcie skuteczne zespolone przez sprzężone natężenie:

S=U*I^*

Jak wykonasz takie obliczeniach na liczbach zespolonych i sprowadzisz wynik do postaci algebraicznej zapisu to otrzymasz, że wynik musi składać się z dwóch członów. Pierwszy będzie liczbą rzeczywistą a drugi będzie liczbą urojoną.

S=P+jQ

Dzięki takiemu zapisowi od razu można ustalić ile jest równa w danym układzie moc czynna a ile jest równa moc bierna. Bardzo przydatne narzędzie :)

Graficznie można to przedstawić w następujący sposób:

Zastosowanie w praktyce – zadanie do rozwiązania

Na koniec, wypróbujmy naszą wiedzę na przykładzie:

Treść zadania: W pewnym obwodzie elektrycznym panuje napięcie skuteczne 230V. W obwodzie wydziela się moc czynna 400W oraz płynie tam prąd o wartości skutecznej 2,5A. Oblicz przesunięcie fazowe oraz amplitudę napięcia i natężenia.

Z treści zadania znamy wartość mocy czynnej, dlatego od razu przypomnijmy sobie wzór na moc czynną

P=U*I*cosφ=R*I² [W]

P=Re{S} [W]

W tym zadaniu jednym z poleceń jest napisane że mamy obliczyć kąt przesunięcia fazowego między napięciem i natężeniem. We współczynniku mocy czyli w elemencie cosφ mamy kąt między napięciem a natężeniem. Tak że na pewno ten pierwszy wzór nam się przyda. Wszystko w nim znamy bo moc czynną znamy z treści zadania, napięcie i natężenie skuteczne również. Poniżej podstawiłem dane i otrzymałem kąt.

Druga część zadania jest jeszcze łatwiejsza. Mamy obliczyć amplitudę napięcia i natężenia. Amplituda czyli inaczej wartość maksymalna. Jak to można obliczyć? Jeśli masz do czynienia z przebiegiem sinusoidalnym to wystarczy wymnożyć wartość skuteczną przez pierwiastek z 2 i po sprawie. Gdybyśmy mieli do czynienia z przebiegiem trójkątnym to trzeba byłoby to wymnożyć razy pierwiastek z 3.

Rozwijaj swoją wiedzę z nami!

Chcesz dowiedzieć się więcej? Nie czekaj, odwiedź mój kanał na YouTube! Znajdziesz tam pełno przydatnych informacji oraz praktycznych przykładów, które pomogą Ci lepiej zrozumieć tajniki elektrotechniki.

Link do filmu: Zrozumienie mocy czynnej, biernej i pozornej

A jeśli naprawdę chcesz zgłębić temat, zapisz się na mój kurs online! Dzięki niemu zdobędziesz solidną wiedzę z podstaw elektrotechniki i teorii obwodów.

Link do kursu: Podstawy elektrotechniki i teorii obwodów