Praca, Moc, Energia: Fizyka, która Cię rozbawi i rozkręci Twoje życie!

Czy kiedykolwiek zastanawiałeś się, co mają wspólnego praca, moc i energia? Oprócz tego, że brzmią jak wymówki, które podajemy, żeby nie iść na siłownię, są to kluczowe pojęcia w fizyce. Ale nie martw się! Dzięki temu artykułowi dowiesz się wszystkiego w sposób lekki, przyjemny i z humorem. Praca, moc i energia To są jedne z najważniejszych pojęć w fizyce, bo co by tutaj ukrywać, są one w pewnym sensie bezpośrednio związane z finansami. Za energię i wykonaną pracę trzeba zapłacić, żeby uzyskać jakąś określoną moc. A dzisiejszy świat stoi na pieniądzach, więc czego by się nie dotknąć wszyscy będą zadawali pytania właśnie o te 3 pojęcia.  Z tego powodu również i my nie możemy ich pominąć w naszym omówieniu.Zaczynajmy!

Wzór na pracę: Oto jak możesz obliczyć, ile wysiłku włożyłeś w życie

Praca mechaniczna jest wykonana tylko i wyłącznie wtedy, gdy do ciała przyłożymy jakąś siłę i ta siła spowoduje przesunięcie ciała na jakąś odległość.

Najprostszy przypadek mamy wtedy, gdy i kierunek siły i przesunięcie jest takie same, bo wartość siły można wówczas obliczyć mnożąc wartość siły razy wartość przesunięcia. Wynik otrzymamy w dżulach.

W=F*r [J]

W- praca

F- wartość siły

r- droga przemieszczenia

Dżul – Twój nowy ulubiony przyjaciel od mierzenia wysiłku

Jeden dżul to tyle pracy, ile potrzeba, żeby przesunąć ciało o masie 1N (Newtona, nie psa) na 1 metr. Tylko uważaj – siła i przesunięcie muszą iść w tę samą stronę. Inaczej? No cóż, nie zrobisz ani jednego dżula i będziesz musiał zacząć od nowa.

Cały czas podkreślam, że kierunek i zwrot musi być taki sam, w przeciwnym wypadku nie będziemy mogli korzystać ze wzoru powyżej. Dlaczego tak jest?

Prawdę mówiąc siła i przemieszczenie to są wielkości wektorowe, więc nasz wzór powinniśmy zaczynać od podania wzoru wektorowego, czyli tej najbardziej podstawowej wersji. Jeśli operujesz na wektorach to należy powiedzieć, że praca to jest iloczyn skalarny siły i przemieszczenia.

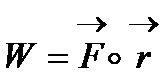
Z matematyki powinieneś pamiętać, że iloczyn skalarny 2 wektorów można zapisać, że jest to długość pierwszego wektora razy długość drugiego wektora razy cosinus kąta między nimi.

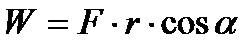
Jeśli kąt między siłą a przemieszczeniem jest równy 0, tzn. przemieszczenia i siła mają ten sam kierunek i zwrot, a w takim przypadku cosinus kąta 0^o jest równy 1 i wzór na pracę przyjmuje postać:

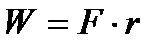
Teraz sprawa się wyjaśniła. Sam zobacz na rysunek

W=F*r*cosa=5*3*cos0^o=15J

Praca i energia - czym się różnią? 

Praca i energia są to wielkości podobne, bo i jedno i drugie podaje się w dżulach. Jaka jest jednak między nimi różnica? Jeżeli ciało ma wykonać jakąś pracę to musi posiadać energię, która zostanie zamieniona na pracę. Tak więc energia jest pewnego rodzaju paliwem pozwalającym na wykonanie pracy.

Rozróżniamy różnego rodzaju energie, nie mniej jednak najbardziej popularną jest energia kinetyczna i potencjalna.

Energia kinetyczna: Moc w ruchu, czyli dlaczego bieganie może być zabójcze (dla Twojej motywacji)

Energia kinetyczna to taki magiczny składnik, który pojawia się, gdy ciało zaczyna się ruszać. Tak, zgadza się – jeśli leżysz na kanapie, to Twoja energia kinetyczna wynosi ZERO. Wzór, za pomocą którego można obliczyć energię kinetyczną to

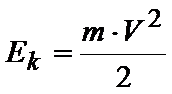
Gdzie:

E_k- energia kinetyczna[J]

m- masa[kg]

V- szybkość[m/s]

Z powyższego wzoru wynika że energia kinetyczna zmienia się wraz z masą jeśli masa ciała rośnie to również jego energia rośnie. Energia zależy również od kwadratu szybkości.

Energia kinetyczna - wyprowadzenie

Jeśli praca i energia to wielkości podobne to spróbujmy wyprowadzić wzór na energię właśnie z pracy.

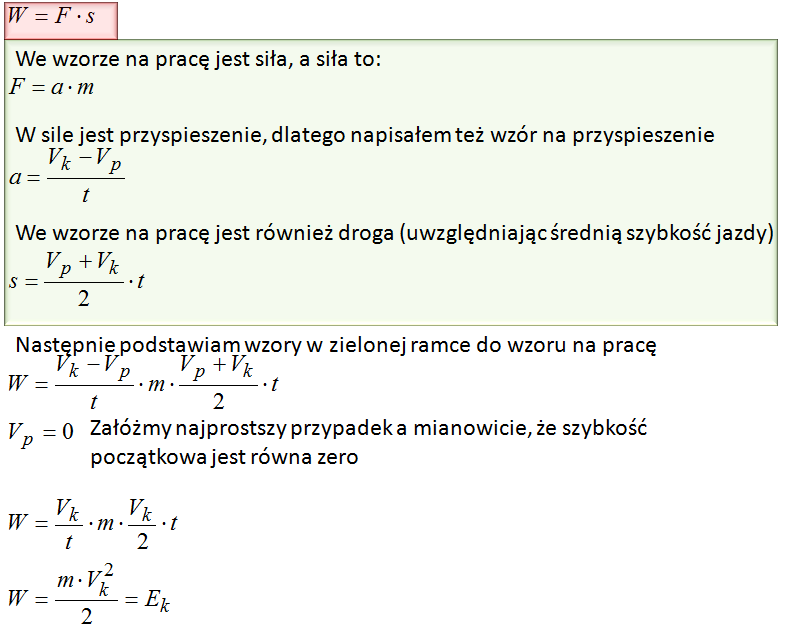
Otrzymałem, że pracę a tym samym również energię kinetyczną można otrzymać z powyższego wzoru.

Energia potencjalna: Wysokość ma znaczenie!

Energia potencjalna to taka ukryta moc, którą zyskujesz, gdy np. wspinasz się na górę. Im wyżej, tym więcej tej energii masz. Zasada jest prosta: podnosisz coś ciężkiego, dajesz mu energię potencjalną. Ale uwaga – jak to upuścisz, ta energia zmieni się w kinetyczną.

Zmianę energii potencjalnej możemy obliczyć ze wzoru:

ΔEp=m⋅g⋅h

Gdzie:

ΔEp – zmiana energii potencjalnej grawitacji
g – przyspieszenie grawitacyjne [m/s^2]

m – masa [kg]
h – wysokość [m]

Zasada zachowania energii: Fizyka nie lubi marnotrawstwa!

Jeśli kiedykolwiek zjadłeś całą pizzę i poczułeś, że energia Cię opuściła – to masz złudzenie! Zasada zachowania energii mówi, że energia nie znika, tylko zmienia swoją formę. Może więc energia z Twojej pizzy właśnie zamienia się w… leżenie na kanapie?

To jak z termosami – jeśli energia jest w układzie zamkniętym, nic nie zginie. Co najwyżej zmieni się w inny rodzaj energii, np. z potencjalnej na kinetyczną. Tak samo jak z węglem – spalasz go, a energia chemiczna zamienia się w cieplną. Proste, prawda?

Tę zasadę można zapisać w następujący sposób:

E=const

Lub inaczej:

E_{początkowa.u.izolowanego}=E_{końcowa.u.izolowanego}

Moc: Więcej mocy, Scottie! Czyli jak szybko wykonujesz pracę

Moc to nie tylko termin używany w „Star Treku”, ale także w fizyce. Oznacza, jak szybko wykonujesz pracę. Czyli – jeśli coś robisz wolno, to Twoja moc jest mała. Jeśli biegniesz szybko do lodówki – moc rośnie! Moc jest to wielkość skalarna (to znaczy,  że nie jest to wektor). Można ją obliczyć dzieląc pracę przez czas.

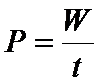
P- moc [W]

W- praca [J]

t- czas[s]

Mam dla Ciebie ciekawe zadanie z zakresu pracy, mocy i energii – znajdziesz je pod tym linkiem: Zadanie online.

Jeśli natomiast zależy Ci na solidnej dawce dobrze wytłumaczonych zadań, to serdecznie polecam mój kurs! W ciągu 6 godzin omówiłem krok po kroku mnóstwo przykładów z pracy, mocy i energii, tłumacząc każdy szczegół. Sprawdź tutaj: Kurs – Praca, Moc, Energia.