Kinematyka: Zrozum ją jak nigdy dotąd!
Czy kiedykolwiek myślałeś, że fizyka to nuda? Czas zmienić zdanie! Kinematyka, czyli nauka o ruchu, może być nie tylko ciekawa, ale i całkiem zabawna! W tym artykule dowiesz się, czym jest układ odniesienia, jak wygląda ruch prostoliniowy i dlaczego nie warto wieźć farby na rowerze!
Co to jest układ odniesienia? Czyli: jak nie zwariować, patrząc na pociągi
Zacznijmy od podstaw. Kiedy analizujesz ruch, musisz wiedzieć, względem czego go analizujesz. Tak, wiem, brzmi to dziwnie, ale wyobraź sobie taką sytuację: siedzisz wygodnie w pociągu, zajadasz kanapkę, a tu nagle – bum! – okazuje się, że względem podłogi pociągu się nie poruszasz, ale względem ziemi? No to już całkiem inna bajka. Jedziesz jak rakieta z prędkością pociągu! A teraz weź sobie kawę i pomyśl, ile razy tobie się to przydarzyło, tylko tego nie zauważyłeś.
Jak zrozumieć układ odniesienia? (Bez straty dla kanapki)
To proste: wszystko zależy od tego, co uznamy za punkt odniesienia. Czy to podłoga pociągu, czy może cała Ziemia. To właśnie od układu odniesienia zależy, czy będziesz Einsteinem fizyki, czy zagubionym podróżnikiem w świecie równań.

Układ współrzędnych: Królowa fizyki, czyli jak nie zgubić się w przestrzeni!
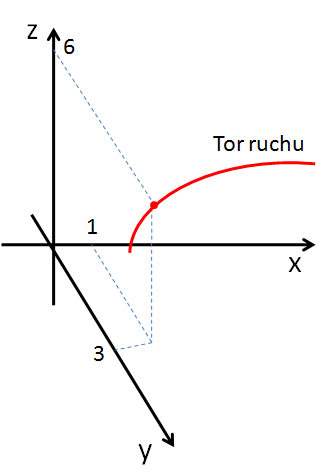
Układ współrzędnych to coś, co pomoże ci ustalić, gdzie dokładnie się znajdujesz (nie, nie chodzi o twoje zagubione skarpetki!). W rzeczywistym świecie każdy punkt można opisać za pomocą 3 współrzędnych – X, Y i Z. Ale spokojnie, na egzaminie raczej wystarczy kartka papieru i dwie współrzędne: X i Y.
3D vs 2D: Gdzie lepiej jechać na rowerze?
Wyobraź sobie, że wieziesz farbę na rowerze (genialny pomysł, co?). Kiedy puszka zaczyna przeciekać, farba tworzy ślad na asfalcie. Ten ślad to twój tor ruchu. I właśnie tor ruchu może być prosty (jak farba na drodze) lub krzywy (jeśli jeździsz slalomem między kałużami). Zabawne? A jak! Ale lepiej nie próbować tego w domu.
Układ współrzędnych 3D
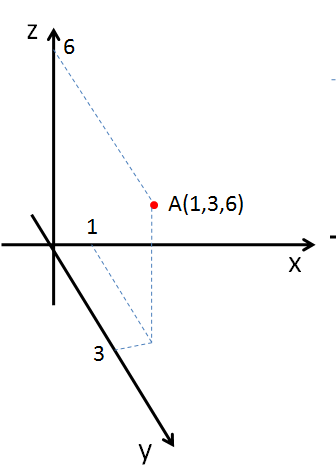
Układ 2D
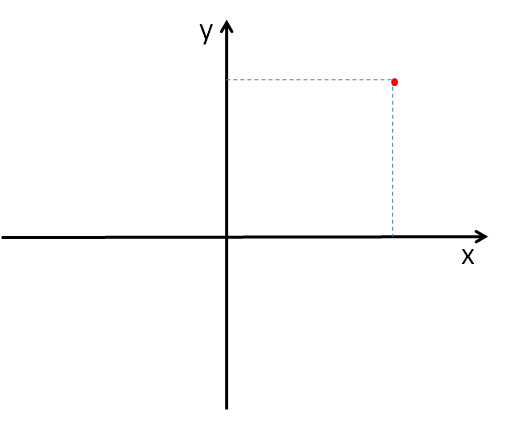
Ruch jednostajny prostoliniowy: Jak jechać bezpiecznie 50 km/h
W ruchu prostoliniowym wszystko jest jasne jak słońce: jedziesz prosto, prędkość się nie zmienia. Np. jadąc z szybkością 50 km/h, po godzinie przejedziesz dokładnie 50 km. Skomplikowane? Nie bardzo, prawda?
Prędkość w ruchu jednostajnym: czyli jak szybko możesz jechać, zanim wpadniesz w kałużę?
Prędkość to taki elegancki wektor – strzałka, która mówi ci, w którą stronę i z jaką szybkością jedziesz. Prędkość jest to wielkość wektorowa ... . Każda regułka zaczyna się dokładnie tak samo, ale co to oznacza? To znaczy, że prędkość możemy przedstawić jako wektor, czyli taką strzałkę. W sumie jest to bardzo wygodne, bo taka strzałka (wektor) od razu nam mówi o kierunku, zwrocie i wartości. Grot strzałki pokazuje zwrot i w sumie również po części kierunek ruchu, natomiast długość wektora mówi o jego wartości tzn. im dłuższa strzałka tym ciało porusza się szybciej.
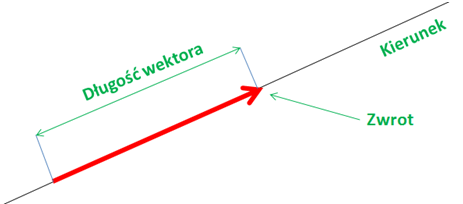
Nie zawsze musi nas interesować zwrot oraz kierunek przemieszczania, czasami interesuje nas tylko sama wartość długości wektora, wtedy mówimy o szybkości. Prosty przykład: każdy szybkościomierz w samochodzie pokazuje tylko wartość szybkości, np. samochód jedzie 120km/h nie pokazuje on zwrotu ani kierunku jazdy. Ta wielkość dla jadącego jest zbędna, dlatego w zupełności wystarcza tylko sama szybkość. Szybkość przedstawiamy za pomocą następującego wzoru:
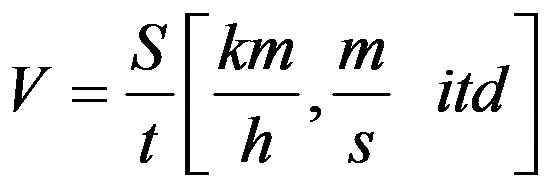
Gdzie:
V- szybkość
S- droga
t- czas
Ruch jednostajnie przyspieszony: Czas na turbo doładowanie!
A co, jeśli zaczynasz przyspieszać? O tak, to już jest coś! Każda kolejna sekunda to coraz większa szybkość. Wartość przyspieszenia obliczasz dzieląc różnicę szybkości przez czas. Proste? Proste! Jak turbo w samochodzie – przyspieszasz, przyspieszasz, a potem... no cóż, lepiej zwolnij, zanim wpadniesz w kłopoty.
W jaki sposób można obliczyć wartość przyspieszenia? Poniżej wzór.
Wartość przyspieszenia
Wartość przyspieszenia możemy obliczyć dzieląc różnicę szybkości przez czas.
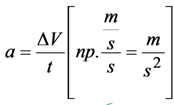
a – wartość przyspieszenia
ΔV=(Vk–Vp)
Vk – szybkość końcowa
Vp – szybkość początkowa
t – czas
Droga w ruchu jednostajnie przyspieszonym: Jak daleko uciekniesz?
Drogę obliczasz za pomocą wzoru. I teraz uwaga – nie martw się, że wygląda groźnie, to po prostu matematyka! A my przecież kochamy liczby, prawda
Każde poruszające się ciało porusza się po jakimś torze ruchu. Znowu przykład! Powiedzmy, że jedziesz na rowerze, a na bagażniku wieziesz przebitą puszkę farby. Ten ślad po farbie pozostawiony na asfalcie jest torem ruchu. Tor ruchu można podzielić na:
- prostoliniowy
- krzywoliniowy
Specjalnym przypadkiem toru krzywoliniowego jest ruch po okręgu.
Droga w ruchu jednostajnie zmiennym
Drogę w takim ruchu możemy obliczyć korzystając z poniższego wzoru.
Podsumowanie: Kinematyka na wesoło – teraz to się rozkręciło!
Kinematyka może brzmieć strasznie, ale jeśli dodasz do niej trochę humoru, wszystko staje się prostsze! Fizyka to nie tylko wzory, ale i zrozumienie świata, który nas otacza. A jeśli jeszcze jesteś głodny wiedzy, zapraszam do naszych kursów:
Nie martw się – obojętnie, na jakim poziomie jesteś, pomogę ci przetrwać tę fizyczną przygodę!




