Równanie van der Waalsa - Gdzie Fizyka Spotyka się z Magią (i Cząsteczkami)
Czy kiedykolwiek zastanawiałeś się, jak wygląda równanie gazu, który tak naprawdę nie istnieje? Brzmi jak science-fiction, prawda? No cóż, fizyka ma dla nas mnóstwo takich niespodzianek. Dziś zajmiemy się jednym z takich cudów - równaniem van der Waalsa. Ale spokojnie, będzie śmiesznie, zrozumiale
Równanie Clapeyrona - Gdzie Wszystko Się Zaczyna
Zanim wskoczymy w zawiłości równania van der Waalsa, musimy cofnąć się trochę w czasie, do równania Clapeyrona, czyli... gazu doskonałego! Tak, to jest ten sam gaz, który istnieje tylko na papierze, w rzeczywistości jego brak. Ale nie szkodzi - fizycy lubią wyobraźnię.
Równanie Clapeyrona wygląda tak:
pV=nRT
Co to oznacza? Ano, że możemy pominąć rzeczywiste oddziaływania między cząsteczkami oraz ich własne rozmiary. Tak, wyobrażamy sobie gaz jako nieskończoną ilość mikroskopijnych kuleczek, które nie oddziałują na siebie, tylko krążą w przestrzeni bez ograniczeń. Fajnie, co?
Równanie Sztywnych Kul - Bo Każda Kula Ma Swoje Granice!
Następnym krokiem w naszej podróży jest... równanie sztywnych kul! Brzmi to jak fizyczny żart, ale to nic innego jak delikatnie zmodyfikowane równanie Clapeyrona. Co się zmienia? Ano to, że dodajemy „nb” do objętości. Co to „nb”? To poprawka na objętość własną cząsteczek gazu. No bo hej, nawet cząsteczki potrzebują trochę prywatnej przestrzeni!
Równanie sztywnych kul wygląda tak:
p(V-nb)=nRT
W ten sposób od objętości dostępnej dla gazu odejmujemy te małe kawałki, które zajmują cząsteczki. Jeśli chcesz poczytać więcej o sztywnych kulach (ha, brzmi to jak wycieczka w kosmos!), zapraszam do wcześniejszego artykułu: Równanie Sztywnych Kul
Równanie van der Waalsa - Fizyka na Sterydach!
Dobra, teraz czas na gwiazdę wieczoru - równanie van der Waalsa! Zróbmy to w stylu superbohatera: „Co by się stało, gdyby... cząsteczki gazu miały swoją objętość i oddziaływały między sobą?”. Brzmi epicko, prawda?
Van der Waals doszedł do wniosku, że gaz rzeczywisty nie działa jak te wyimaginowane, doskonałe gaziki. Nie możemy pominąć objętości cząsteczek ani ich wzajemnych oddziaływań. A co za tym idzie, ciśnienie gazu jest inne niż to, które widzimy w równaniu Clapeyrona.
Podsumujmy: gaz rzeczywisty jest trochę bardziej „skompresowany”, bo cząsteczki mają swoją objętość i... lubią się przytulać! (albo ściskać, jeśli wolisz techniczne terminy).
Po prostu nie da się zignorować faktu, że objętość, w której cząsteczki mogą się poruszać musi być pomniejszona o objętość, którą te cząsteczki zajmują. Dodatkowo w równaniu van der Waalsa wprowadzono również zmiany odnośnie ciśnienia. Dlaczego? A dlatego, że gdy na cylinder z ruchomym tłokiem wywierano nacisk powodując zwiększenie ciśnienia wewnątrz zauważono, że objętość w cylindrze zmniejsza się bardziej niż by to wynikało z równania.
Dlaczego To Ważne?
Wywnioskowano, że przy większych ciśnieniach musi się coś dziać wewnątrz, między cząsteczkami tak, jakby wytwarzało się w środku jeszcze większe ciśnienie, niż te które przykładamy do tłoka, które jeszcze bardziej ściska cząsteczki gazu ze sobą. Dziś już wiemy, że na ciśnienie gazu nie wpływają tylko sprężyste zderzenia cząsteczek, ale również wzajemne oddziaływania między nimi. Z tego powodu w równaniu van der Waalsa do ciśnienia dodano człon, który korygował ciśnienie do wartości poprawnej.
Tak więc zapamiętaj, równanie van der Waalsa wywodzi się z równania Clapeyrona.
Posiada ono tylko poprawkę dotycząca ciśnienia i objętości. W rzeczywistości ciśnienie jest większe niż wynikałoby z równania Clapeyrona przez oddziaływania cząsteczek, natomiast objętość jest mniejsza, ponieważ trzeba jeszcze uwzględnić objętość cząsteczek gazu.
(p+p’)*(V-V’)=nRT
To dodatkowe ciśnienie przedstawia się następującym wzorem:
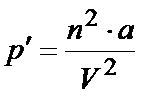
Stała "a" to wielkość charakterystyczna dla danego gazu
V’=nb
b- również jest to wielkość charakterystyczna dla danego gazu.
Finalnie równie van der Waalsa przedstawia się następującym równaniem:
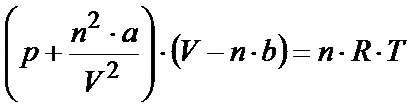
Zastosowanie Równania van der Waalsa - Dla Chemików i Mechaników!
Hej, mechanicy i chemicy, jeśli jesteście spragnieni wiedzy, to poniżej mam coś dla Was! To kursy pełne rozwiązań problemów z termodynamiki i chemii fizycznej. Możecie zgłębić wszystkie te równania na maksa:
- Kurs z Chemii Fizycznej 1A
- Kurs z Chemii Fizycznej 1B
- Kurs z Termodynamiki 1A
- Kurs z Termodynamiki 1B




