Przyspieszenie styczne, przyspieszenie dośrodkowe oraz tor ruchu - Zabawy z Muchą w Akcji!
Wprowadzenie do Przyspieszenia - Czas na Odlotową Przygodę!
Jeśli tutaj trafiłeś to pewnie szukasz czegoś odnośnie przyspieszenia stycznego, dośrodkowego albo toru ruchu. Dobrze trafiłeś. W tym artykule wszystko wytłumaczę, a żeby nie było nudno, posłużę się zabawnym przykładem. W końcu, kto powiedział, że fizyka nie może być śmieszna? Poniżej treść zadania:
Treść zadania: Mucha porusza się zgodnie z funkcją S(t)=So*ec*t gdzie c>0, So>0. Dodatkowo wektor przyspieszenia wypadkowego tworzy kąt φ ze styczną do toru ruchu. Na zajęciach z mechaniki prowadzący poprosił Was abyście obliczyli szybkość muchy, wartość przyspieszenia stycznego, dośrodkowego.
Przyspieszenie Sty... Co? Czyli Wstęp do Tematu z Muchą
Tak jak widzisz to zadanie nie jest takie standardowe jakie być może analizowałeś do tej pory na fizyce. Zakładam, że na fizyce w większości przypadków miałeś podane dane w postaci jakiś konkretnych liczb. Droga przebyta to mogło być np. 10 km, szybkość np. 10m/s. A więc jakieś konkretne liczby. Natomiast w tym zadaniu mamy podaną funkcję przemieszczenia. Na jej podstawie możemy określić jak wyglądał tor, po którym przemieszczała się mucha. Ten tor ruchu jak widzisz jest zależny od czasu (zmienna t). Czas jest w nim zmienną. Chcąc określić dokładnie położenie muchy w danym momencie wystarczy w miejsce czasu wpisać sekundę, w której chcielibyśmy to określić. Nie zawsze musi nas przecież interesować tylko ruch prostoliniowy. Ciała mogą się przecież również przemieszczać po różnego rodzaju krzywych.
Rzut Oka na Tor Lotu Muchy
To może zobrazujmy sobie jak wygląda tor lotu muchy. Z jaką funkcją mamy tutaj do czynienia? Mam nadzieję, że się nie przestraszyłeś tej funkcji. Jest tam liczba „e”, a to oznacza, że mamy do czynienia z funkcją exponencjalną. Tak się nazywają wszystkie funkcje, które zawierają w sobie liczbę e. W matematyce jest coś takiego jak liczba p ona jest równa około 3,14 , ale oprócz tego są jeszcze inne tego typu liczby np. liczba „e”. Jej wartość to mniej więcej 2,72. A więc w tym zadaniu mamy sytuację, że liczba 2,72 jest podniesiona do potęgi i w tej potędze jest zmienna t (w matmie byłaby to zmienna x, natomiast w fizyce może to być np. czas tak jak w tym zadaniu). Takie coś to przecież nic innego jak funkcja wykładnicza. Funkcja wykładnicza może wyglądać jak poniżej:
W naszym zadaniu przy zmiennej „t” stoi „C” , które jest większe od zera (tak wynika z treści zadania). Skoro tak to tor ruchu musi wyglądać jak pokazuje to ta czerwona linia. Po takim torze będzie przemieszczała się mucha.
Obliczanie Szybkości - Na Pełnym Luzie
Zacznijmy nasze obliczenia od szybkości, a właściwie od funkcji szybkości, bo otrzymamy wynik w formie funkcji. W jaki sposób się obliczało szybkość do tej pory? Wystarczyło podzielić drogę przez czas, i gotowe. W zadaniach, w których są funkcje wygląda to nadal prawie tak samo, z tą małą różnicą, że trzeba podzielić nieskończenie małą zmianę drogi przez nieskończenie małą zmianę czasu co w praktyce oznacza, że trzeba będzie zrobić pochodną z danej funkcji.
V=ds/dt
Podstawmy w miejsce S w powyższym wzorze funkcje naszej drogi i zróbmy pochodną po czasie.
Funkcję szybkości udało nam się obliczyć. Podstawiając w miejsce czasu jakąś konkretną sekundę ruchu można ustalić z jaką szybkością wówczas przemieszczała się mucha. Graficznie można to przedstawić tak jak poniżej:
Szybkość zawsze jest styczna do toru ruchu. Pierwsze polecenie już mamy rozwiązane, teraz zastanówmy się jak obliczyć przyspieszenie styczne. Generalnie przyspieszenie styczne i dośrodkowe ( tego typu wielkości) oblicza się w ruchu po okręgu. My natomiast nie mamy tutaj ruchu po okręgu tylko ruch po krzywej. Jak w takim razie obliczyć te wielkości? Czy to w ogóle jest możliwe?
Przyspieszenie Styczne - Skok do Matematyki
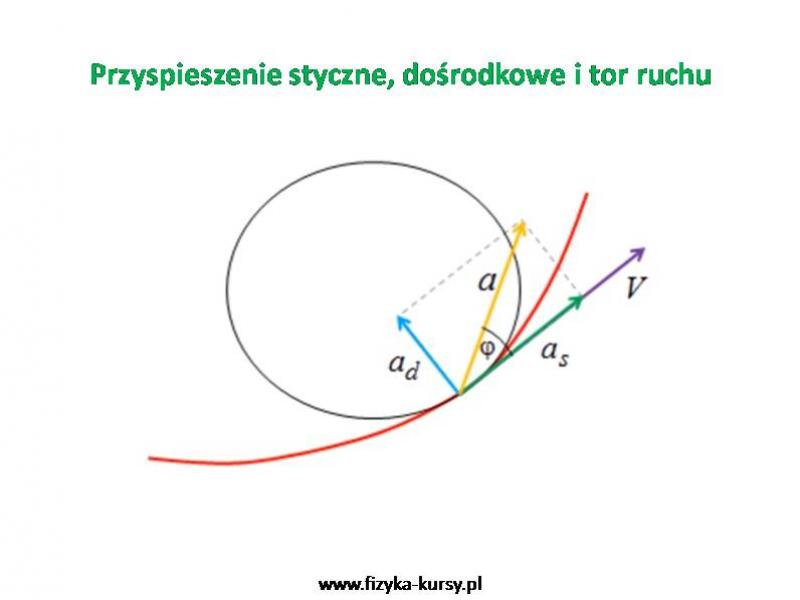
No więc tak, jak weźmiemy mały wycinek naszego toru ruchu to można go spokojnie wpisać w okrąg (inaczej mówiąc dopasować do okręgu). W takim razie można również na tym małym wycinku wpasowanym w okrąg obliczyć takie wielkości jak przyspieszenie styczne i dośrodkowe. Graficznie można to przedstawić tak jak poniżej:
Już wiemy jak jest skierowana prędkość styczna. W takim razie przyspieszenie styczne musi mieć dokładnie taki sam kierunek. Właśnie dlatego jest na tej samej linii co prędkość.
Oprócz tego w ruchu po okręgu mamy również przyspieszenie dośrodkowe, którego zwrot zawsze jest w stronę środka okręgu. Oba te przyspieszenia można zastąpić przez jedno przyspieszenie wypadkowe „a” , które jest sumą obu wcześniejszych. Kąt między przyspieszeniem wypadkowym a stycznym jest równy f.
W jaki sposób obliczyć as? Odpowiemy sobie najpierw na pytanie jak się oblicza wartość przyspieszenia? Trzeba podzielić szybkość przez czas a=V/t. Jeśli pytają nas o wartość przyspieszenia stycznego to trzeba podzielić szybkość styczną (już ją obliczyliśmy) przez czas. W naszym przypadku operujemy funkcjami więc trzeba podzielić nieskończenie małą zmianę szybkości przez nieskończenie małą zmianę czasu. Wynik poniżej
Przyspieszenie Dośrodkowe - Kiedy Mucha Zakręca
Najczęściej wartość przyspieszenia dośrodkowego obliczamy korzystając z poniższego wzoru:
W powyższym wzorze należy w miejsce szybkości wstawić szybkość styczną (to akurat już obliczyliśmy) i podzielić to przez promień okręgu. Promienia okręgu jeszcze niestety nie znamy, tak że za pomocą tego wzoru na pewno nie uda nam się obliczyć ad.
Wartość przyspieszenia dośrodkowego można obliczyć korzystając z trygonometrii. Wartość kąta fi znamy, przyspieszenie styczne również. Bez problemu obliczymy ad.
Znając już ad oraz V można by wrócić do wzoru na przyspieszenie dośrodkowe i obliczyć również promień okręgu, jeśli byłoby to potrzebne w tym zadaniu.
Podsumowanie i Zaproszenie do Dalszej Zabawy
To zadanie możesz znaleźć na moim profilu na YouTube. Zapraszam do obejrzenia rozwiązania!
Dodatkowo zapraszam do skorzystania z mojego kursu online z kinematyki punktu. Znajdziesz tam więcej takich zadań. Kliknij w grafikę poniżej, żeby dołączyć!