Energia swobodna i entalpia swobodna – czyli jak naukowcy upraszczają życie, a nam je komplikują!
Po energii wewnętrznej, entalpii i entropii, przyszedł czas na kolejne gwiazdy termodynamicznego show – energię swobodną i entalpię swobodną. Jeśli zastanawiasz się, dlaczego dodajemy do tej skomplikowanej układanki jeszcze więcej funkcji, to... cóż, witaj w świecie nauki! Im więcej równań, tym weselej – znaczy, prościej (przynajmniej w teorii!). I zanim pomyślisz, że to żart, obiecuję – to faktycznie ma sens!
Czym jest energia swobodna i entalpia swobodna?
Energia swobodna to taka „dobra część” energii, którą można zamienić na pracę lub ciepło w warunkach stałej objętości. Entalpia swobodna? To podobna bajka, tylko przy stałym ciśnieniu. Więc jeśli masz do czynienia z sytuacją, w której nic nie eksploduje i ciśnienie nie rośnie jak w filmach akcji – będziesz częściej korzystać z entalpii swobodnej.
Dlaczego te funkcje są takie ważne?
Obie te funkcje to taki termodynamiczny kompas. Pomagają nam określić, czy dany proces przebiega samorzutnie, czy raczej nic z tego nie będzie. Jasne, mogłeś to robić wcześniej za pomocą entropii (pamiętasz entropię, prawda?), ale tutaj pojawia się pewien problem...
Jeśli suma entropii układu i otoczenia była równa zero to proces był odwracalny.
dSukł+dSoto=0
Natomiast jeśli większa od zero to proces był samorzutny i nieodwracalny.
dSukł+dSoto>0
Entropia i jej problematyczne otoczenie
Problem z entropią polega na tym, że uwzględnia ona entropię otoczenia, a kontrolowanie tego, co dzieje się w „otoczeniu”, to jak próba kontrolowania... pogody. No, trudna sprawa! Dlatego naukowcy stwierdzili, że muszą coś z tym zrobić i wpadli na pomysł – zamieńmy to otoczenie na coś prostszego! I voila, mamy energię swobodną i entalpię swobodną! Warto było trochę pogłówkować, bo przecież umiejętność określania czy procesy są samorzutne czy nie jest bardzo przydatna.
Jak to wyprowadzono?
Zanim zaczniesz kręcić nosem, że „jeszcze więcej równań”, daj mi szansę. Naukowcy wzięli pierwsze równanie, przekształcili je i – tadam! – doszli do wniosku, że zmiana entropii otoczenia to -zmiana entropii układu. Sprytne, prawda?
dSoto=- dSukł
Wyprowadzanie krok po kroku
Jak wiesz na zmianę entropii układu wpływa produkcja entropii oraz transport entropii
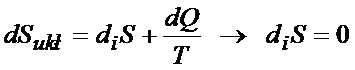
W warunkach odwracalnych produkcja entropii jest równa zero, wówczas zmiana entropii układu jest równa:
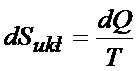
Teraz trzeba się zastanowić czemu jest równe ciepło w warunkach stałej objętości ( zerknij na wzór poniżej)
dU=dQ+p*dV
Oczywiście dV czyli zmiana objętości w warunkach stałej objętości jest równa zero nie ma żadnej zmiany objętości). Z tego wynika, że ciepło jest równe dU=dQ
Jak już wiemy ile jest równe ciepło to możemy je wstawić do zmiany entropii układu.
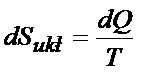
Na początku tego artykułu napisałem, że dSoto=- dSukł teraz znając już dSukł spokojnie możemy napisać, że zmiana entropii otoczenia jest równa:
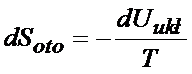
Jak już mamy zmianę entropii otoczenia to możemy wrócić do drugiej nierówności w tym artykule, a mianowicie:
dSukł+dSoto>0
I w miejsce dSoto wstawić wyprowadzoną zależność:
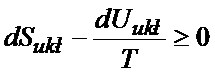
Poniżej wyprowadzenie już do końca wzoru na energię swobodną:
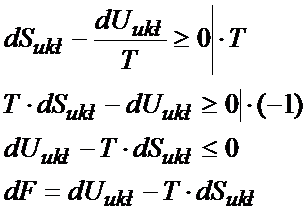
Jeśli dF jest mniejsze od zera to proces jest samorzutny. Tak samo można wyprowadzić wzór do entalpii swobodnej.
Poniżej są rozpisane definicje na energię swobodną i entalpię swobodną oraz wzory, z którego można obliczyć zmianę energii swobodnej i entalpii swobodnej.
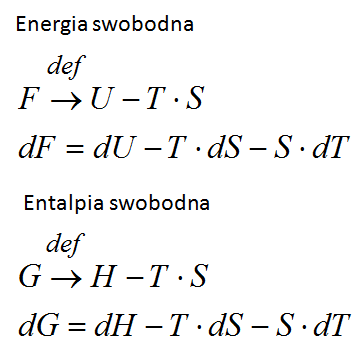
Podsumowanie: Energia swobodna i entalpia swobodna
Na koniec – jeśli po tych wszystkich równaniach jeszcze się trzymasz, gratulacje! Wiemy już, jak wyprowadzić wzory na energię swobodną i entalpię swobodną. Obie te funkcje pozwalają nam określić, czy procesy przebiegają samoczynnie, a to naprawdę przydatna sprawa w chemii, fizyce i w ogóle w naukowym życiu.
Chcesz więcej?
Jeśli to Cię jeszcze nie przekonało, zapraszam do mojego kursu, gdzie znajdziesz zadania z tej tematyki. Link poniżej!





