Różniczka zupełna energii wewnętrznej

Poniżej przedstawiam wzór na różniczkę zupełną energii wewnętrznej. Nie ma co ukrywać, ale w zasadzie to właśnie on jest najczęściej wykorzystywany na obliczeniach z chemii fizycznej. Dobrze, już się dowiedziałeś, że w praktyce to właśnie ten wzór jest bardzo istotny. Pytanie tylko dlaczego on tak wygląda? Skąd się biorą w nim te pochodne, wartości bezwzględne itd. ?

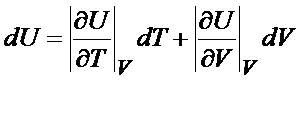
Żeby to zrozumieć to trzeba wrócić na chwilę do matematyki, bo właśnie tam znajdziemy odpowiedź na to pytanie. Wytłumaczę to na przykładzie:

Powiedzmy, że chcesz wyznaczyć objętość kuli

Objętość można obliczyć korzystając ze wzoru:

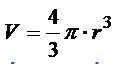
Żeby za pomocą tego wzoru obliczyć objętość to musimy wziąć suwmiarkę i zmierzyć jej średnicę. Wzór na objętość to jest tak naprawdę funkcja i można ją narysować:

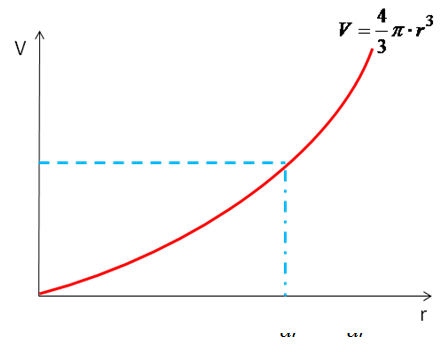
Znając promień można z wykresu odczytać jaką kula ma objętość (patrz na niebieskie linie przerywane).

Ale jak wiadomo suwmiarka mimo iż robi dokładne pomiary to jednak mierzy z dokładnością do 1 podziałki, a to oznacza, że ten nasz promień może być o niewielką wartość większy lub mniejszy od tego co zmierzyliśmy.

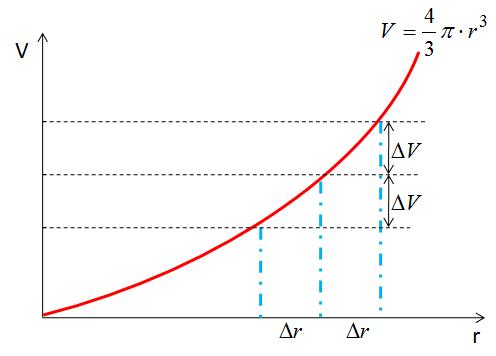
Ok. Skoro promień może się różnić o jakąś wartość to objętość również jest zawarta w jakimś przedziale. Pytanie, jak można obliczyć o ile może się ta wartość różnić od wartości rzeczywistej? Najlepiej zrobić styczną do funkcji.

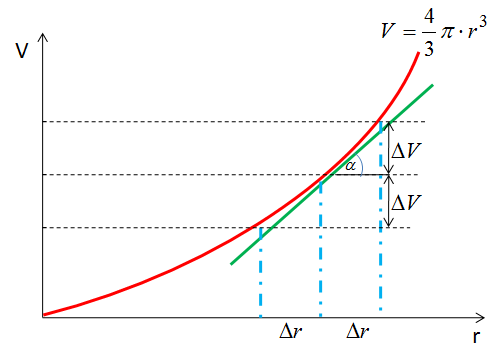
W wyniku czego otrzymaliśmy na wykresie trójkąt prostokątny, który jest nachylony pod kątem alfa. Jeden z jego boków ma długość „Δr” a drugi „ΔV”. „ΔV” właśnie chcemy obliczyć. To jest akurat proste, bo wystarczy skorzystać z tangensa kąta alfa.

W poniższym wyprowadzeniu zastanawiające było tylko to jak obliczyć tangens kąta alfa? Generalnie współczynnik liniowy prostej, czyli tangens kąta alfa jest równy pochodnej. Wystarczy więc zrobić pochodną z funkcji objętość po zmiennej „r”

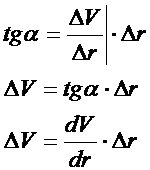
W tym przypadku analizowaliśmy sytuacje, w której mieliśmy tylko jedna zmienną „r”. A jak wiesz funkcja może mieć więcej zmiennych i wówczas do każdej zmiennej trzeba napisac różniczkę zupełną. Poniżej taki przykład:

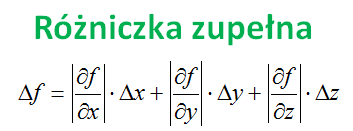
Jak się zsumuje wszystkie takie elementy to się otrzyma całkowitą maksymalną różnicę funkcji z jaką możemy ją obliczyć. W zapisie na różniczkę supełną są wartości bezwzględne, bo ten wzór na maksmalny bład musi uwzględniać również najgorszy scenariusz, a mianowicie, że błędy się sumują. Dzięki czemu uzyskujemy wynik największego możliwego do osiągnięcia błędu (lub inaczej mówiąc równicy) pomiaru gdy  wszystkie te różnice się do siebie dodadzą.

Właśnie z tego powodu we wzorze na różniczkę zupełną są wartości bezwzględne. Oczywiście w miejscu Δx, Δy, i Δz mogą stać nieskończenie małe zmiany czyli „dx”, „dy” i „dz” , czyli różniczki.

Ok. Już wiesz skąd się bierze różniczka zupełna i że można ją wykorzystać np. do obliczenia różnicy między stanem początkowym a końcowym, albo do obliczenia błędu pomiaru. Dlaczego to pojęcie wykorzystujemy również do energii wewnętrznej? A dlatego że bezwzględnej wartości (całkowitej wartości) energii wewnętrznej nie jesteśmy w stanie obliczyć, bo tak naprawdę nie jesteśmy w stanie zsumować wszystkich rodzajów energii jakie się znajdują w ciele.

To co jednak jesteśmy w stanie określić to to że np. ciało ma wyższą albo niższą energię choćby poprzez to, że ma wyższą albo niższą temperaturę.

Krótko mówić jesteśmy w stanie obliczyć różnicę energii między jakimś stanem A a stanem B , a jak wiesz do obliczania różnicy wykorzystuje się różniczkę zupełną.

Tak więc jak chcesz obliczyć ΔU to musisz skorzystać z różniczki zupełnej. Patrząc na wzór na I zasadę termodynamiki łatwo ustalić,  że zmiana energii wewnętrznej następuje na skutek dostarczonego ciepła oraz wykonanej pracy objętościowej.

ΔU=Q+W

Z tego wynika, że wielkościami, które się mogą zmieniać w energii wewnętrznej są temperatura oraz objętość (zmiana energii wewnętrznej zależy od pracy objętościowej).

A skoro tak, to żeby obliczyć różniczkę zupełną dla energii wewnętrznej to trzeba ją uzależnić od tych zmiennych.

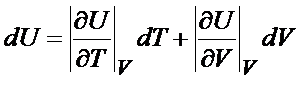
Właśnie z tego powodu wzór na różniczkę zupełną energii wewnętrznej wygląda właśnie w taki sposób.

Znając już te podstawy nie będziesz mieć problemów,  żeby napisać wzór na różniczkę zupełną entalpii albo energii wewnętrznej. Jedyne co musisz w ich przypadku wiedzieć to jakie parametry w danej funkcji się zmieniają.

Jeśli ten temat  interesuje Cię bardziej to zachęcam do odwiedzenia mojego kursu wideo, w którym znajdziesz obliczonych mnóstwa zadań z tej tematyki. Ten kurs to chemia fizyczna 1b.