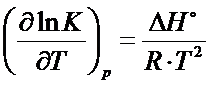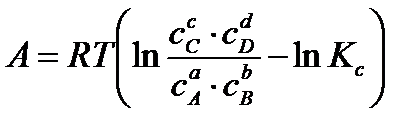Izobara van’t Hoffa

Jacobus van’t Hoff zaproponował kilka równań, które łączyły ze sobą stałą równowagi reakcji, temperaturę i efekt energetyczny reakcji. Tymi równaniami są izobara van’t Hoffa

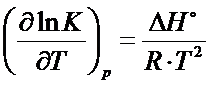
i izochora van’t Hoffa.

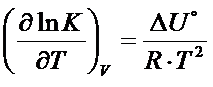
Opracował on jeszcze izotermę van’t Hoffa

Jeśli chodzi o izobarę  van’t Hoffa i izochorę to dużo większe znaczenie dla chemików ma ta pierwsza. Być może zastanawiasz się dlaczego? A dlatego, że większość doświadczeń jakie się przeprowadza są w stałym ciśnieniu. Obrazowo mówiąc układy o stałym ciśnieniu to najczęściej otwarte reaktory, w których panuje ciśnienie atmosferyczne, które podczas doświadczenia ma stałą wartość (a więc się nie zmienia).  Zdecydowanie rzadziej stosuje się układy zamknięte, w których mamy ściśle określoną objętość. Ciśnienie w takich układach zmienia się wraz ze zmianą temperatury (temperatura rośnie--> ciśnienie rośnie, temperatura maleje --> ciśnienie maleje).

Za pomocą Izobara van’t Hoffa można określić wpływ temperatury na stałą równowagi reakcji przy stałym ciśnieniu. Poniżej wyprowadzenie wzoru na izobarę van’t Hoffa:

1. Najpierw trzeba zacząć, że izobara porównuje stałe równowagi K_p1 i K_p2 z dwóch różnych temperatur T₁ i T₂. Do tej pory zawsze jak chcieliśmy porównać jakieś 2 stany to wystarczyło od stanu drugiego odjąć stan pierwszy. Tym razem też tak zrobimy. Z tego powodu najpierw wyprowadzimy równanie dla temperatury T₁ , a potem takie samo dla temperatury T₂ poczym jedno równanie odejmiemy od drugiego.

Jednym z najważniejszych pojęć w  chemii to entalpia swobodna. Gdy układ znajduje się w równowadze to można obliczyć standardową entalpię swobodną reakcji na 2 sposoby:

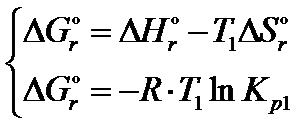
Po przyrównaniu obu wzorów do siebie otrzymujemy zależność jak poniżej

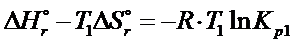
To równanie można tak przekształcić, żeby logarytm ze stałej ciśnieniowej był po lewej stronie równania, a cała reszta po prawej.

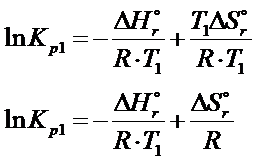
Dokładnie takie same równanie można wyprowadzić do temperatury T₂

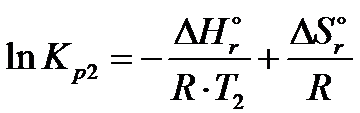
Następnie tak jak już napisałem wcześniej należy odjąć od siebie logarytmy ze stałych ciśnieniowych K_p2 i K_p1. Po kilku przekształceniach ostatecznie dojedziemy do izobary van’t Hoffa, która przedstawia zależność między stałymi ciśnieniowymi, temperaturą a standardową entalpią danej reakcji

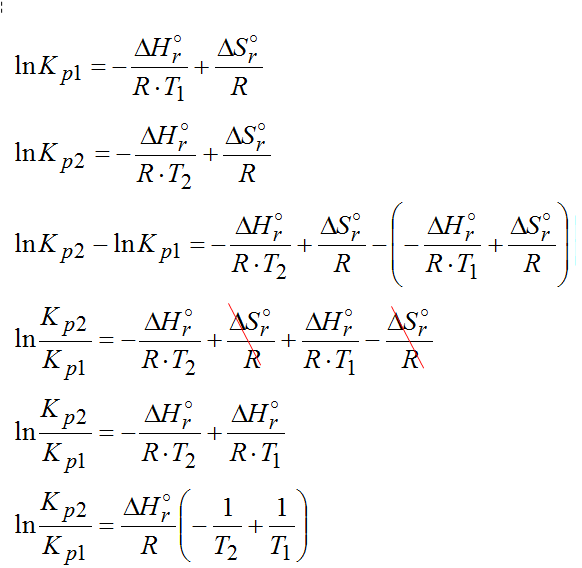
Ten wzór można też przedstawić w sposób różniczkowy. Wówczas wygląda on tak: