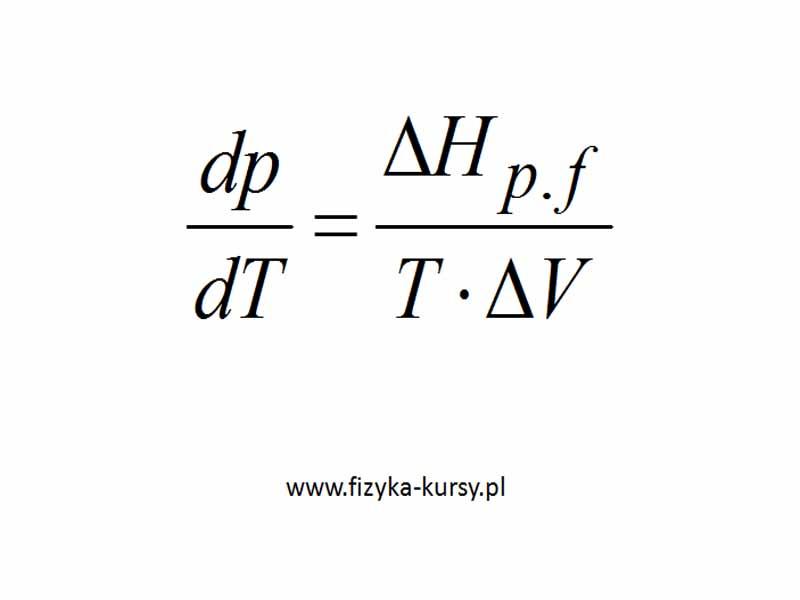Równanie Clausiusa-Clapeyrona
Poniżej znajduje się wzór na najbardziej popularną postać równania Clausiusa-Clapeyrona.
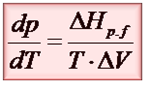
Od razu chciałbym Ci jednak powiedzieć, że nie jest to jedyna postać. Dla przemiany fazowej typu cieczà gaz. W takiej przemianie tą druga objętością jest gaz, a jak wiadomo objętość gazów jest dużo większa od objętości cieczy. To stwierdzenie ma kluczowe znaczenie. Dlatego dla tego typu przemian równanie Clausiusa-Clapeyrona można zapisać na dwa różne sposoby:
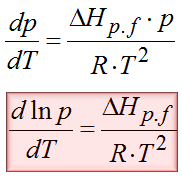
Wzory już poznałeś, czas dowiedzieć się skąd się to wszystko bierze. Zacznijmy od tego, że równanie Clausiusa-Clapeyrona jest wykorzystywane do opisu wykresów fazowych, a wykresy fazowe dla przemian jednoskładnikowych znajdują się w układzie ciśnienia i temperatury. Tak więc te linie zaznaczone na czerwono na rysunku poniżej (granice faz) są to funkcje ciśnienia i temperatury.
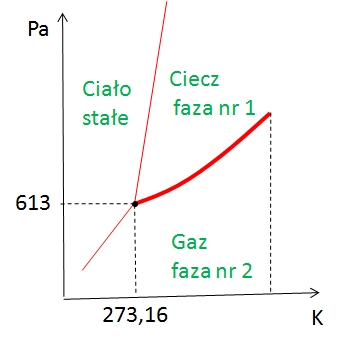
Jeśli chcemy wyprowadzić równanie opisujące te linie równowagi fazowej to na pewno musimy skorzystać z funkcji, która wiązałaby w sobie i zmianę temperatury i zmianę ciśnienia a oprócz tego odnosiłaby się do równowagi. Funkcją, która spełnia wszystkie te trzy warunki jest entalpia swobodna. Różniczka zupełna entalpii swobodnej jest poniżej. Natomiast pochodne w tej entalpii są odpowiednio równe –S i V.
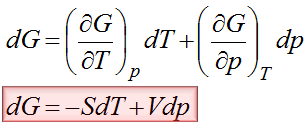
Na linii równowagi fazowej stykają się ze sobą dwie fazy. Do każdej z nich osobno można napisać wzór na zmianę entalpii swobodnej.

Otrzymaliśmy tym samym już właściwą postać wzoru. Jest jednak ona trochę mało praktyczna, bo we wzorze powyżej znajduje się zmiana entropii. Dużo przyjemniej pracuje się na entalpii, a poza tym entalpie mamy stabelaryzowane. Jak wygląda wzór łączący ze sobą zmianę entalpii i entropii dla przemiany fazowej? Poniżej przedstawiłem tę zależność.
ΔSp.f= ΔHp.f/Tp.f
Po podstawieniu powyższego wzoru w miejsce zmiany entropii otrzymujemy następującą postać równania Clausiusa- Clapeyrona.
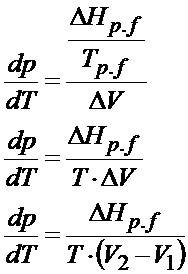
Otrzymaliśmy tym samym chyba najbardziej popularną postać równania Clausiusa Clapeyrona. To jednak jeszcze nie koniec. Można to jeszcze bardziej rozwinąć. Załóżmy, że analizujemy sytuację przemiany fazowej między cieczą a gazem. W takiej sytuacji objętością V1 jest objętość cieczy natomiast V2 to objętość gazu. Objętość gazu zawsze jest dużo większa od objętości cieczy czy ciała stałego, dlatego jeśli z delty V wyrzucimy V1, która jest bardzo mała w porównaniu z objętością gazu, to na skutek tego uproszczenia błąd jaki popełnimy będzie zaniedbywalnie mały. Dodatkowo jeśli jeszcze założymy, że mamy do czynienia z gazem doskonałym to objętość 2 będzie można przedstawić za pomocą równania Clapeyrona. Po podstawieniu równania Clapeyrona to otrzymujemy następującą postać dla przemiany Ciecz à Gaz
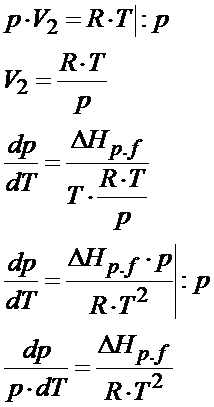
To jeszcze nie koniec dywagacji. Można to jeszcze nieco inaczej zapisać. Zależność dp/p to jest znane w matematyce przejście, które można zastąpić przez dlnp. Pamiętasz jeszcze z matematyki taką zależność? dx/x=dlnx ? Teraz się ona tutaj przyda. Po skorzystaniu z powyższej zależności otrzymujemy następującą postać wzoru Clausiusa- Clapeyrona.
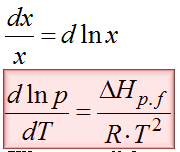
Każda z postaci tego wzoru będzie nam przydatna do swobodnego poruszania się w tej tematyce.
Więcej na ten temat dowiesz się w moim kursie Równowagi fazowe w układach 1 składnikowych
https://fizyka-kursy.pl/kurs/rownowagi-fazowe-w-ukladach-jednoskladnikowych