Reguła Dźwigni – Jak ją rozgryźć i dlaczego to wcale nie takie trudne?

Czy kiedykolwiek miałeś wrażenie, że fizyka to taki nieznośny kolega, który zadaje Ci za dużo trudnych pytań? A teraz jeszcze coś takiego jak reguła dźwigni w diagramach fazowych? Spokojnie! Już ją znasz, bo to nic innego jak stara, dobra dźwignia, którą pewnie widziałeś na lekcji fizyki. Dźwignia jest jak pizza – każdy kęs wydaje się skomplikowany, ale ostatecznie jest pysznie prosta.

Czym jest reguła dźwigni?

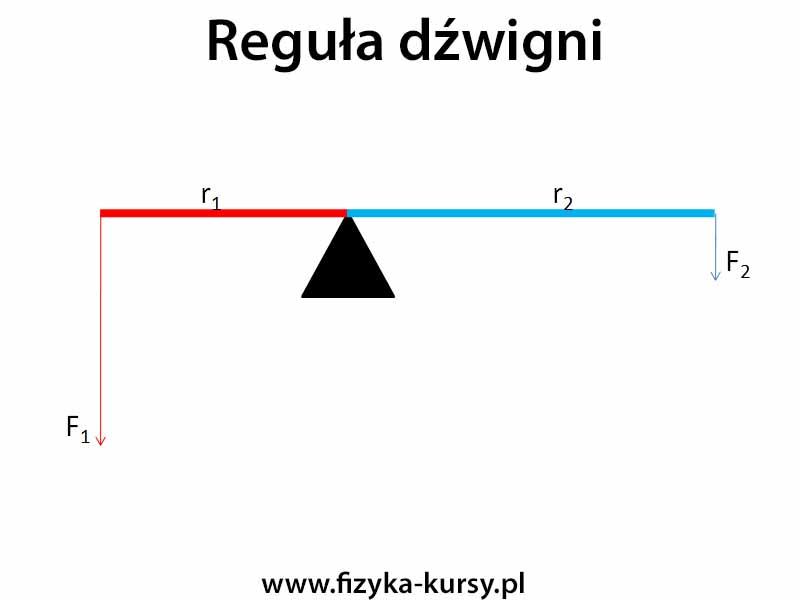
Jeśli układ znajduje się w równowadze to znaczy, że momenty siły czerwonej strony i niebieskiej muszą być równe. Jeśli momenty się zrównoważą to układ pozostanie nieruchomy. Poniżej napisałem równanie, z którego wynika, że momenty są sobie równe.

F₁*r₁=F₂*r₂

Jak wykorzystać regułę dźwigni w diagramach fazowych?

A teraz hit: reguła dźwigni działa nie tylko w najprostrzej fizyce, ale również w… diagramach fazowych! Powiem Ci, jak to działa: masz wykres, na którym masz stężenie i ciśnienie (lub temperaturę). Gdzieś między dwiema liniami (czerwoną i niebieską) znajduje się nasz ulubiony punkt C. I teraz magia – możemy obliczyć, ile mamy fazy α, a ile β, używając… (trzymaj się) reguły dźwigni!

Przykładowy diagram fazowy w układzie ciśnienie w funkcji stężenia p=f(c) przedstawiłem poniżej. Oczywiście również dobrze wykres fazowy może być przedstawiony jako temperatura w funkcji stężenia T=f(c). 

Znowu dźwignia, ale w diagramach fazowych!

Teraz uwaga! W dźwigni w fizyce musieliśmy wymnożyć długość ramienia, razy siła, jaka działała na końcu ramienia. W diagramach fazowych jest podobnie. Długość czerwonego ramienia jest równa (c-c_a), natomiast niebieskiego tyle (c_b-c).

Jeśli chodzi o długość ramienia dźwigni sprawę mamy już załatwioną. A co jeśli chodzi o siłę na końcu ramienia? Co ją zastępuje w tym układzie? W tym układzie zastępuje ją masa!

Skąd wiem, że należy tutaj wprowadzić masę? Do obliczenia długości ramienia wykorzystaliśmy stężenie procentowe! Ze stężeniem procentowym związana jest masa. Wynika to bezpośrednio ze wzoru na stężenie bo przecież w liczniku i w mianowniku tego wzoru znajduje się masa ( patrz na wzór poniżej).

Jak sam widzisz, rzeczywiście ze stężeniem procentowym bezpośrednio związana jest masa. Z tego powodu w tym przypadku „siłą” działająca na końcu ramienia tym razem musi być masa. Dlatego długość ramienia tym razem mnożę razy masę.

m- masa

c- stężenie procentowe

Dźwignia a ułamki molowe – Co tu się dzieje?!

W przypadku gdy na osi „x” w diagramie fazowym są ułamki molowe to długość ramion mnożę razy liczbę moli. Dlaczego? A no dlatego, że ułamki molowe bezpośrednio są związane z liczbą moli ( tak jak pokazuje to wzór poniżej). W ułamku molowym wykorzystuję liczbę moli, a więc w tym przypadku „siłą” działająca na końcu ramienia musi być liczba moli.

Z tego powodu w układach, w których wykorzystujemy ułamki molowe, wzór na regułę dźwigni musi wyglądać tak:

n- liczba moli

x, y – ułamki molowe

Czasami w zadaniach trzeba dokładnie pokazać ile się ma fazy alfa, tzn. ile procent w danym punkcie mamy fazy alfa a ile fazy beta. Jeśli mamy podać stężenie procentowe jednej z faz to na pewno do tego celu przyda się wzór na stężenie procentowe.

Wcześniej już wyprowadziliśmy wzór na stosunek jednaj fazy do drugiej:

W następnym kroku możemy masę alfa wprowadzić do wzoru na stężenie procentowe w wyniku czego otrzymujemy to:

Masy fazy beta nam się poskracały.

Finalnie otrzymaliśmy wzór za pomocą, którego moglibyśmy obliczyć ile procent mamy fazy alfa. Warto zauważyć, że jak chcesz obliczyć stężenie procentowe fazy alfa to w liczniku wstawiasz długość odcinka będącego bezpośrednio przy fazie beta (niebieski odcinek). Jeśli natomiast chciałbyś obliczyć stężenie procentowe fazy beta to w liczniku musiałaby być długość odcinka czerwonego, czyli odcinka, który jest bezpośrednio przy fazie alfa.  Znając już te podstawy można zrealizować 2 zadania.

Zastosowanie reguły dźwigni w praktyce – Zróbmy to razem!

Zadanie 1: Ile procent mamy cyny, a ile ołowiu?

Zastanów się jaki mamy skład w czerwonym punkcie?  Tzn. ile procent mamy cyny a ile ołowiu.

Zapamiętaj koniecznie, że do odczytywania składu nie potrzebujemy reguły dźwigni tylko odczytujemy to dokładnie z osi X. W tym przypadku widać, że czerwony punkt na osi X jest gdy ołowiu mamy 70% a cyny 30%.

Zadanie 2: Obliczamy procentową zawartość fazy ciekłej i stałej

Wyznacz ile masz fazy ciekłej ( w %) a ile stałej w czerwonym punkcie. Oraz oblicz jaką masz zawartość składników w fazie ciekłej i fazie beta.

Skład odczytujemy bezpośrednio z osi „x” natomiast żeby obliczyć procentową zawartość fazy w punkcie to musimy skorzystać z reguły dźwigni. Korzystając ze wzoru, który wyprowadziłem wcześniej jeśli chcesz obliczyć procentową zawartość fazy ciekłej oznaczonej literką L, to w liczniku musisz wstawić długość odcinka będącego przy fazie b, a w mianowniku wstawić całkowitą długość odcinka:

Na danym odcinku zawartość fazy ciekłej i fazy beta jest równa 100%, więc jeśli fazy ciekłej mam 27% to znaczy że fazy beta mam resztę, czyli 73%

Teraz musimy jeszcze zająć się zawartością. Jak już wiesz zawartość należy odczytać z osi „x”. Jeśli chcesz odczytać jaką masz zawartość w fazie ciekłej to musisz spojrzeć na miejsce gdzie rozpoczyna się faza ciekła na badanym odcinku, ona rozpoczyna się w miejscu gdzie ołowiu mamy 38%, tak więc to jest zawartość ołowiu w fazie ciekłej. Resztę, czyli 62% mamy cyny.

W fazie b mamy 82% ołowiu i 18% cyny. Zadanie zakończone:)

Podsumowanie – Dźwignie są wszędzie!

Dźwignia to nie tylko fizyka – to życie! Mimo że mogła wydawać się skomplikowana, teraz jest już jasne, jak działa w diagramach fazowych. Wystarczy trochę matematyki i odrobina humoru, a każda reguła staje się przyjemniejsza.

Tego typu zadania możesz znaleźć w moim kursie z „Równowaga fazowa w układach dwuskładnikowych” Poniżej link: https://fizyka-kursy.pl/kurs/rownowagi-fazowe-w-ukladach-dwuskladnikowych